LED通信事業プロジェクト　エンジニアブログ

高校生でもわかる通信用語 #5

デシベルってなに？

記事更新日 2024年2月27日

---

社内の人間に、「今までのブログは難しすぎて専門家しか読まないよ」と指摘されて始めた「高校生でもわかる通信用語」シリーズの第5回です。できるだけ難しい言葉を使わずに、できるだけわかりやすく通信用語を説明していきたいと思います。

はじめに

通信を勉強すると「デシベル（dB）」という単語が頻繁に出てきます。この言葉、本来は電力や電圧を表す単位であって、厳密な意味での通信用語ではないのですが、特に無線通信をする上では絶対に避けることことができない単語です。また、デシベルは、電気関係の他にも、音関係とか光関係でも使われます。例えば、工事現場で「ただ今の騒音○○デシベル」みたいな表記を見たことがある人も多いと思います。

このように、結構暮らしに密接なデシベルなんですが、デシベルって何って検索するも、数式が並んでいて撃沈、そんな人も多いはず。というわけで、今回は「デシベル」という単語を、なるべく式を使わずに紹介していこうと思います。

空間中を伝わる「波」の性質

さて、先ほどデシベルよくが使われるのは、無線（電波）、音、光といいました。これら3つの共通点ってわかりますか？

わかりますよね。いずれも「空間中」を伝わる「波」です。そして、これらを扱うときにデシベルが必要となります。それは何故か？　簡単です。一言で言えば、空間中の波はむちゃくちゃ減衰するからです。波は空間中を伝わる際にとてもとても減衰します。もう普通の数字で扱うことが難しいほどに小さくなっちゃうんです。

それは、電波や光、音などのエネルギーが「距離の二乗に反比例」するからです。例えば、1mから10mに離れると、1mの時と比較して、エネルギーは10の2乗分の1、すなわち100分の1になってしまいます。1mから10mなんて、そんな大きな距離じゃ無いですよ？歩いても数秒。それなのにエネルギーは100分の1です。じゃあ、100mならどうなるか？1kmならどうなるか？そう考えていけば、距離の二乗に反比例っていうのが、とてもとても数字を小さくしてしまうってことが、なんとなくわかって貰えると思います。

さて、なぜエネルギーが距離の二乗に反比例するのか？これも比較的簡単ですので、光を例にして説明いたします。

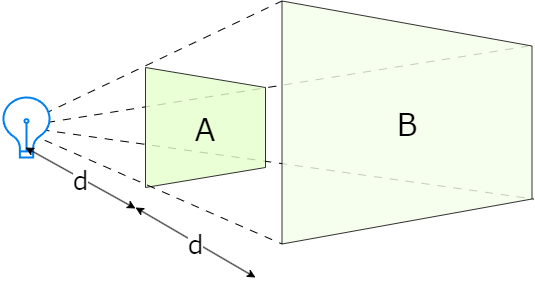
例として、プロジェクターがスクリーンに画像を映しているとしましょう。プロジェクターからdの距離にあるスクリーンをAとします。スクリーンをAからさらにd離した距離、つまりプロジェクターから2d離した距離のスクリーンをBとします。

プロジェクターから出る光の強さは同じなので、スクリーンの位置に限らずスクリーンに映る画面の光の総量、言い換えると画面の光のエネルギーの総量^※1は同じですよね？ということは、Aに当たる光のエネルギー量と、Bに当たる光のエネルギー量は同じはずです。しかし、エネルギー量は同じでも、画面としてはAの方が圧倒的に明るく見えるはずです。

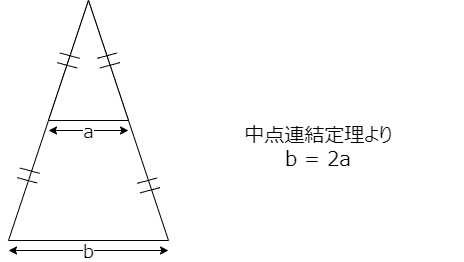
さて、AとBの距離は、Aとプロジェクターまでの距離と同じ。そうなると、四角い画面の一辺の長さは中点連結定理により2倍になります。中点連結定理、中学三年生で習うみたいなんですが、原理は理解しているけど定理の名前を忘れちゃっている人も多いのでは？うん、私もすっかり忘れていてググりました・・・　話を元に戻すと、辺の長さが2倍になるということは、面積は長さの二乗ですから4倍になるということです。AとBはトータルでは同じエネルギー量な訳ですから、Bの単位面積あたりのエネルギーは1/4になるはずです。つまり、同じ面積でも光の量は1/4。そうなると、Bの見た目の明るさはAの明るさの1/4、つまりAのほうが4倍明るいという事になります。言い換えると、AとBで画面全体の総エネルギー量が同じであっても、面積辺りのエネルギーの多いAの方が画面を明るく感じるはずです。

光だけじゃ無くて、音も伝播も同じです。面積辺りのエネルギーが大きい程、明るく、大きく、強く感じます。なぜ、総エネルギーでは無く、単位面積あたりのエネルギーで判断されるのか、それも説明しておきます。

光の場合、強さを感じるのは「瞳」です。「瞳」の大きさって常に一定ですよね？もちろん、瞳孔が開くとかそういうことはありますが一旦無視して、瞳の面積というのは常に一定だと言えると思います。そして、人間が感じる明るさというのは、瞳の面積に入る光の量です。そこに存在する、光の総量ではありません。ですから、瞳の面積辺りの光の量こそが、人間の感じる明るさとなります。

光が瞳の大きさなのだとしたら、音の場合は耳の大きさで、電波の場合はアンテナの大きさである、と言い換える事ができます。最終的に受け取れる本当のエネルギー量は受け取る側の面積に依存します。大きな耳の人は、より沢山の音を集めることができるでしょうから、個人差はあります。でも、強さの評価としては同じ面積で受け取れるエネルギー量、すなわち「単位面積あたりのエネルギー量」を考えるのが適当なんですよね。

まあ、面倒な事をいろいろ書きましたが、光も、音も、電波も、波としてエネルギーが空間を伝わることを考えるときは、そのエネルギーは面積で考えるんです。波の面積は光源や音源から距離が離れるほど広がっていきます。音も電波もプロジェクターの画面と同じとイメージしてください。先ほどの例では距離が2倍になったから、面積は4倍になりました。これを一般的な値にすれば、距離がx倍になれば、面積はx²倍になる、と言えます。すなわち、面積は距離の二乗倍になるわけで、だとすれば到達するエネルギーは「距離の二乗分の1」になるのです。

波のエネルギーをグラフで表す

さて、これまで空間中の波のエネルギーは距離の二乗分の1になる、つまりは距離の二乗に反比例するということを説明してきましたが、じゃあ、実際どれぐらいの強さになるのか？どれぐらい減衰するのか？というものをちょっと計算してグラフにしてみます。前回、TBSラジオの話をしたので、TBSラジオAM放送の電波を考えてみます。

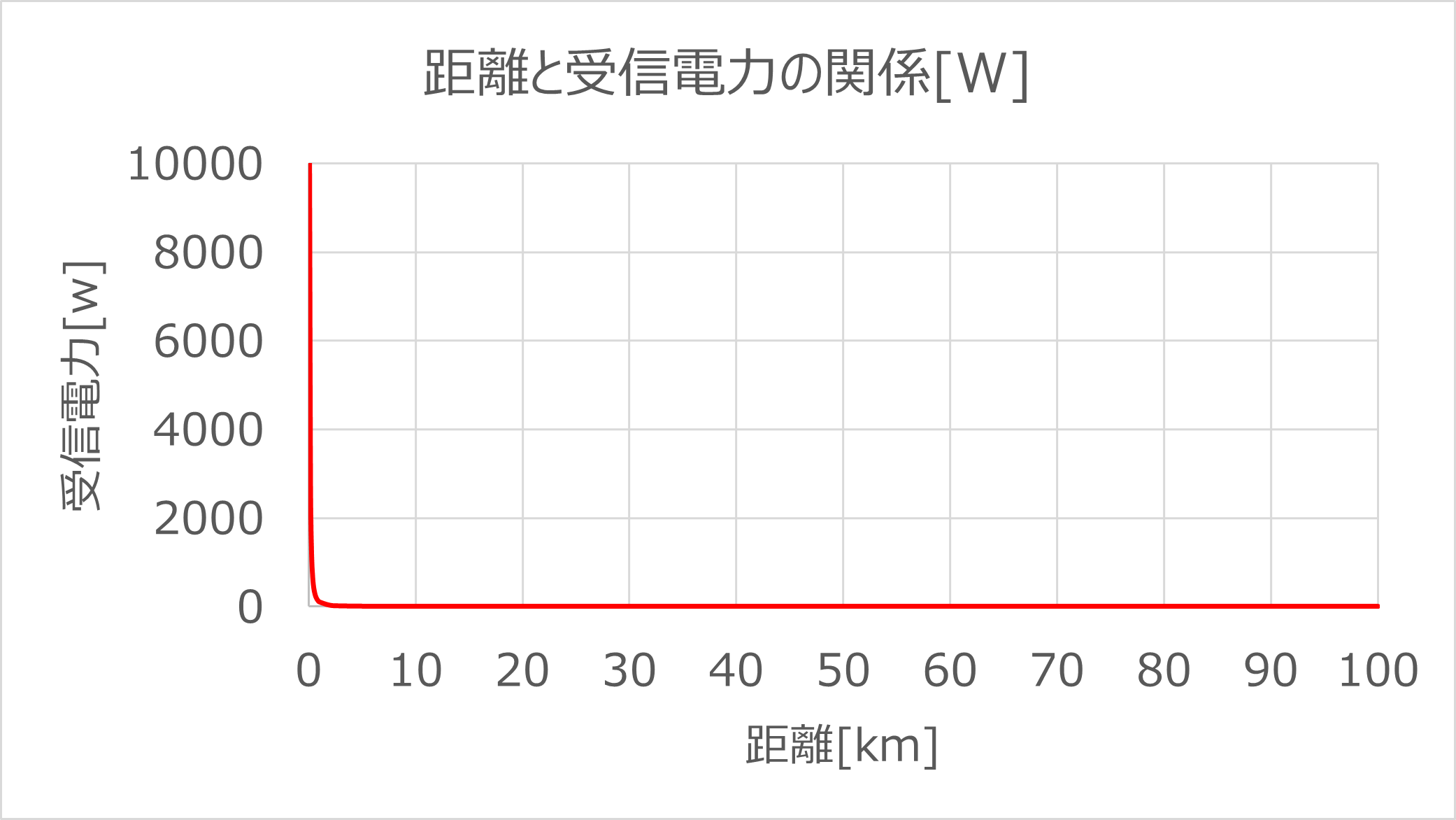
TBSラジオなので周波数は954kHzで出力が100kWです。これを半波長ダイポールアンテナを使用して空間に出したときを考えます。距離によってどれぐらいのエネルギー、電波の場合なので「どれくらいの電力」になるか？をグラフにしたのがこれです^※2。

どうですか？距離100mぐらいまで1万Wぐらいを維持するのですが、3kmを超えると10W程度になり、10kmを超えれば1Wを下回り、30kmを超えると0.1Wを下回ります・・・　って、そんなこと計算した元の数値を見ているからわかるだけで、このグラフだけをみてそんな事読み取れる訳無いですよね？それでは、このグラフから何を理解すればよいか・・・　1kmを超えたら、ほぼ0になるから使えない？　ラジオ向け電波ですからそんなはず無いのですが・・・

もちろん、グラフ上では0Wに見える場所も、実際の数値は0.1Wとか小さな値で、その強さでもラジオは聞こえます。ちなみに携帯電話（電話機側）の最大出力は0.2Wですので、0.1Wは決して弱くないということはご理解頂けると思うのですが、だとしても0.1をグラフに書いてしまうと0にしか見えません。それは、グラフの最大値が10000Wであるためで、10000Wと0.1Wを同じグラフで比べるっていうのは現実的ではありません。

波のエネルギーって、場合によって最大値と最小値を比較し一万倍やら十万倍を超えてしまうんです。だから、波の強さは普通のグラフでは表現できない、ということになります。

デシベルに変換

こういう、変化が大きい、それこそ「桁違い」になるような数値を扱うとき、数学的には対数を使います。特に、音、電波、光のような空間中の波のエネルギーを扱う場合は、「常用対数に10をかけた数字、すなわち10log₁₀X」で計算することになっています。それで計算し直した値は、デシベルという単位になります・・・

と、「デシベル」の説明をするとこのようになるのですが、これで理解できるなら誰も困らないですよね？　本記事は「高校生でもわかる通信用語」です。当然、もっと簡単に式を使わずに説明します。

前章でも書いたとおり、1万から0.1まで扱うとなると、そのままでは値の大小がわかりにくい。なので、変化の幅が大きい尺度に置き換えます。変化の幅が大きいと言ってもよく分からないと思いますので、さらに簡潔に言いましょう。

光や音や電波のように扱う数字の数が馬鹿でかいときは、デシベルという単位を使います。デシベルの意味は次の通りです。

デシベルは桁の「0の個数」に10をかけた数字で表現する

基準は0の個数です。桁数ではありません。10なら1個x10で"10"。100なら2個x10で"20"。10000なら"40"、という感じです。一方、0.1のように小数点になると0の個数はマイナスになります。0.1の場合は-1個x10で"-10"、0.01なら-2個x10で"-20"といった感じです。1はどうなるかというと、1は0個X10で"0"として扱います。

例に出てきたTBSラジオの出力は100,000Wなので5個x10で「50デシベル」です。デシベルの単位はdBと表記されるので"50dB"と書きます^※3。

さて、さっきからキリのよい10000だか、10だかの数字しか話していませんでした。じゃあ、15とか200とか中途半端な数字だったらどうするのでしょう？　その時は・・・　関数電卓なりExcelなりを使って計算して下さい。一発で答えが出ます。今の時代、スマートフォンが関数電卓代わりになりますから、素晴らしい世の中ですよね。いつでもどこでもデシベルが計算できる！（しないか・・・）

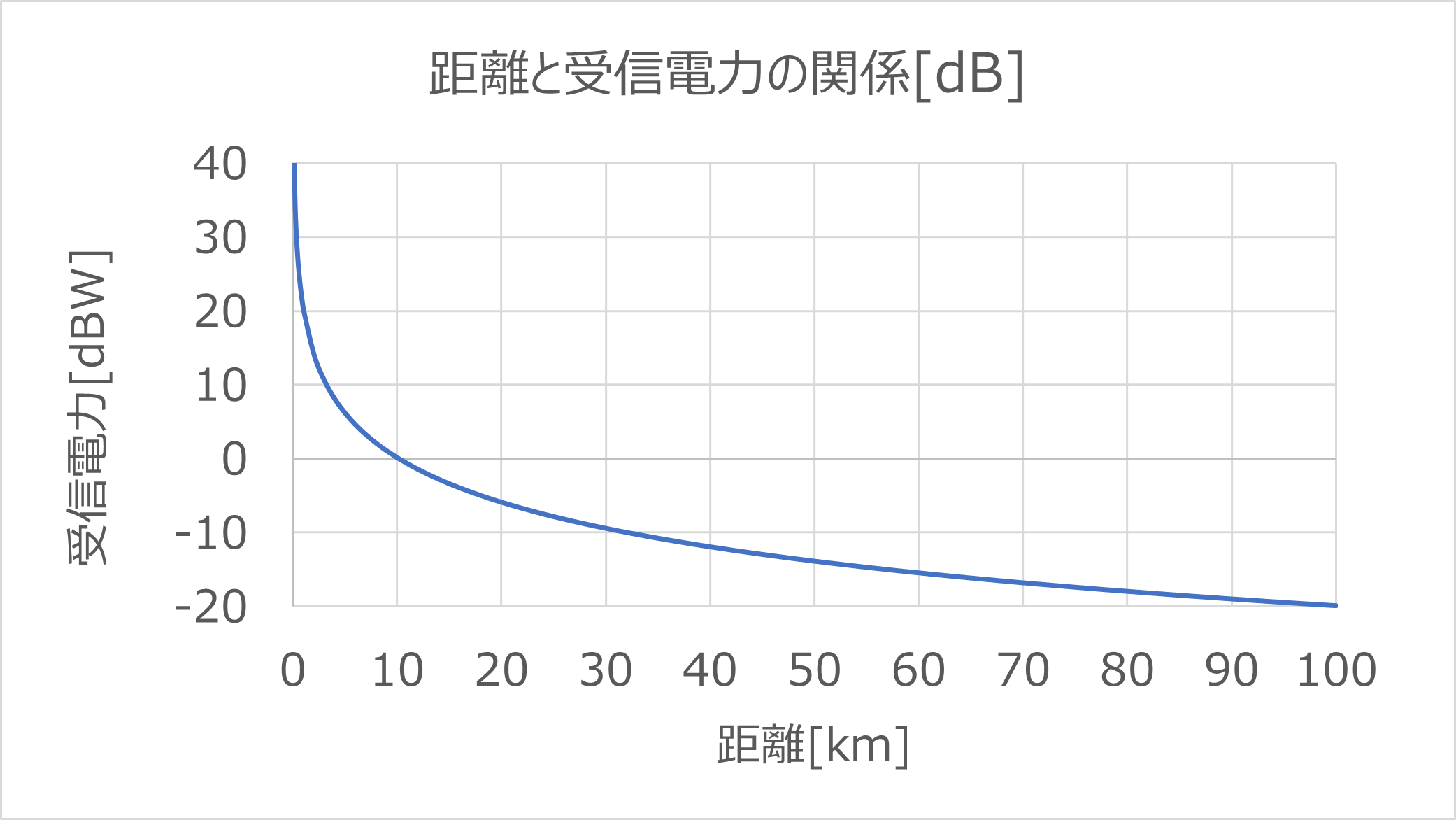
というわけで、デシベル。仕組みは意外に簡単だったと思います。そして、先のTBSラジオのグラフをデシベルに直したグラフで表現するとこうなります。

ほら、グラフっぽくなったでしょ？これなら数値が読めますよね。さて、最初に赤線のグラフを出した時に書いた内容を例に取ります。覚えてないと思いますが、こんなことを言っていました。

3kmを超えると10W程度になり、10kmを超えれば1Wを下回り、30kmを超えると0.1Wを下回ります・・・

これ、赤線グラフだと読み取れなかったんですが、このグラフなら読み取れるんですよね。受信電力10Wすなわち10dB辺りの距離は、およそ3km程度です。また、距離10kmでの受信電力は0dBなので1W程度、30kmでの受信電力は-10dBなので、0.1W程度と読むことができます。このように、「波」の値をデシベルに変えることによって、グラフを読み取り、値を知ることができるというわけです。

デシベルのもう一つの効果

数学的原理はここでは書きませんが、もともとの数値（真数と呼びます）における乗除算（かけ算・割り算）は、デシベルに変換することで加減算（足し算・引き算）にすることができます。例えば、こんな状態があったとします。

• 出力：100,000W
• アンテナの利得：1.64倍
• 距離による減衰：1/2500

この結果の電力を求めるには100,000 × 1.64 ÷ 2500をしなければいけません。うーん、手計算だと面倒。これを全ての数値をデシベルに直している場合はこうなります。

• 出力：50dBW
• アンテナの利得：2.15dB
• 距離による減衰：-34dB

ここから電力を求めるには50 + 2.15 - 34を計算すればよくなります。足し算・引き算だけなので、暗算でもできます。

いろいろと計算するとわかるのですが、距離による減衰やアンテナの利得など波に関する計算は「乗除算」となる事がほとんどです。で、波関連計算は、これまで取り上げた通り扱っている数が極端に大きかったり、もしくは極端に小さかったりしますし、これをかけ算、割り算するのはちょっと厳しいです。今はコンピューターもお手軽ですし、多少桁が多かろうがミスなく計算することができますが、手計算の場合は・・・　5桁と4桁のかけ算とか、不可能では無いですがやりたくないですよね？　だから、全ての関連数値をあらかじめデシベル変換してから扱うことで、必要な計算が足し算・引き算になって簡単に計算できるのです。

更に言うと、2倍=約3dBと覚えておくだけで、おおよその数字が出せるようになります。例えば、200Wなら、100 x 2ですから、デシベルでは20 + 3となり23dBとなります。800Wなら、100 X 2 × 2 × 2ですから、20 + 3 + 3 + 3で29dBとなります。また、50Wなら、100 ÷ 2ですから、20 - 3で17dBとなります。このように、2倍=3dBを覚えておくだけで、おおよそのデシベルを手計算で求めることができます。

このようにデシベルの計算って、一見コンピューターがないと厳しいように感じますが、厳密では無いおおよその値でよければ、比較的に簡単に暗算できるんです。というか、デシベルって元々は計算機の無い時代に、馬鹿でかい値を扱うために考え出された手法ですので、そもそも普通に計算するより簡単になるように作られているものなのです。機械・電気系を目指す理系の方は、是非手計算にも挑戦してみてください。試験では電卓不可の場合もありますからね。

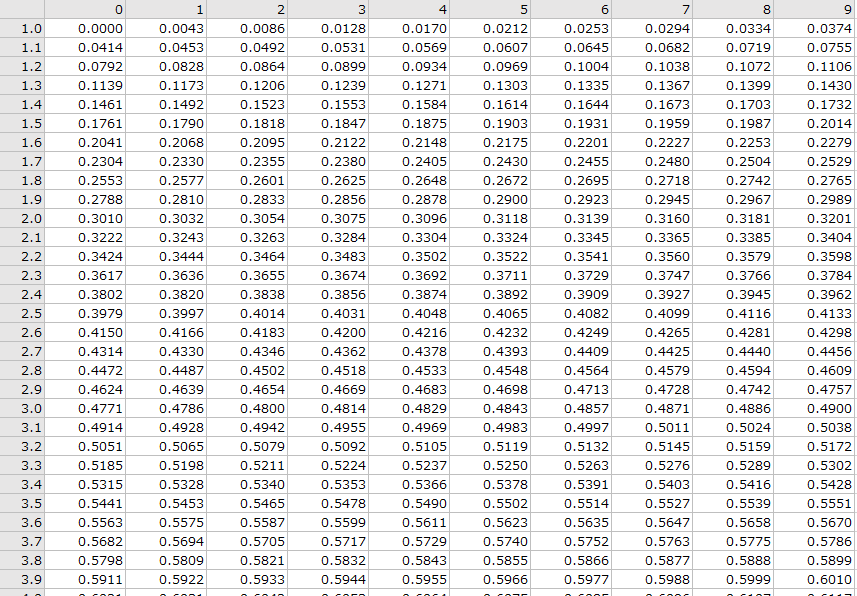
ちなみに、コンピューターの無い時代に、詳細なデシベル計算をしたいときはどうしていたでしょうか？実は、昔は「対数表」というあらかじめ対数が計算されている表があって、コンピューターが無い時代はこれを参照して、詳細なデシベルを計算していたんです。例えば、表の縦軸2.5/横軸0.2の値は0.4014ですが、これはlog₁₀2.52の値を意味します。この0.4014を使えば、2.52W=4.014dBと計算することも、さらに10倍して25.2W=14.014dBと計算することもできます。このように、昔は対数表を使っていたんですよね。昔は教科書の巻末に載ってたりしたんですが、今でもあるんでしょうか？

まとめ

とにかく、でかい数字はデシベルを使えば計算ミスが減ります。「1＋1は2じゃないぞ。オレたちは1＋1で200だ。10倍だぞ10倍！」と間違えて、未だに馬鹿にされている人がいますが、あらかじめ「1＋1は3dBじゃないぞ。オレたちは1＋1で23dBだ。」としておければね。23-3なら、さすがのテンコジも間違えることはなかったでしょう・・・

冗談はさておき、デシベルの意味はご理解頂けたと思います。デシベルは日常生活でも結構でてきます。特に音の大きさ表記は街中でもテレビでもよく見かけますが、意味が分かっている人少ないように思えます。デシベルを理解していれば、大声選手権なんかで「ああ、あと6dB足りなかった、惜しい」とか言っているのを見ても、「6dB=4倍なんだけど、惜しいのか？」とか思えるようになるとか、数値に対して正しい判断ができるようになります。最近も聞かない日がないという、地震の「マグニチュード」という単位も、デシベルの亜種みたいなものですしね。デシベルがわかればマグニチュードの理解も簡単です。そんなこんなでデシベル。よく出てきます。習うより慣れろで、とにかく使ってみてください。

それでは、次回をお楽しみに！

---