LED通信事業プロジェクト エンジニアブログ
フレネルゾーンってなに?
記事更新日 2022年9月20日
はじめに
光無線通信のメリットの一つに狭いところを通して通信できるというものがあります。光は、建物の間とか天井裏とか目で見える隙間さえあれば問題なく通信できるのですが、電波だとそういった場所だと大きく減衰してしまい、速度が落ちるか、最悪通信できなくなります。これは、電波と光のフレネルゾーンの違いが影響しているからです。このフレネルゾーン、その定義はいたってシンプルなんですが、何故そうなるのかまでを普通の人(物理が得意ではない人)向けに説明をしているものってなかなか見つかりません。なので今回は光無線通信のメリットを説明してくれる単語「フレネルゾーン」について、その理論を「できるだけ易しく」「誰でも理解できるように」解説していきたいと思います。
フレネルゾーンの成り立ち
歴史
フレネルゾーンは19世紀のフランスの物理学者オーギュスタン・ジャン・フレネル(Augustin Jean Fresnel)にちなんで付けられた名前です。フレネルは光の反射、屈折、回折の研究で、様々な業績を残しています。例えば、反射率や屈折率を計算する式(CGとかで使われる)を発見したり、灯台で使われるフレネルレンズ※1を発明したりしています。ちなみに、我々が販売しているLEDバックホールにもフレネルレンズが使われています。フレネルは光、特に光の波としての性質の研究に生涯を捧げています(病弱だったため39歳の早世)。
波といえばもう一人有名なのが、クリスティアーン・ホイヘンス(Christiaan Huygens)。皆さんも高校時代の物理でホイヘンスの原理って習いましたよね?平面波であっても、波は球面波の集合体である、というやつ。この波がどうやって伝搬するかを解析したのがホイヘンスであり、その名は定理に残っていますが、実はそのホイヘンスの原理を後年補強したのがフレネルなんです。ですから、その定理は現在はホイヘンス=フレネルの原理とも呼ばれています。そして、ホイヘンス=フレネルの原理を踏まえると、光、そして電波はある一定の範囲を持って伝達されるはずだ、というのがフレネルゾーンの原点となります。(以降「ホイヘンス=フレネルの原理」だと長いので、単に「ホイヘンスの原理」と呼びます)
ホイヘンスの原理
ホイヘンスの原理によると、2点間を伝わる波は見た目だと直線上を通っているように見えて、実はそうでない・・・ 習ったはずなのに覚えていないですか?覚えていないという方のために、ホイヘンスの原理を改めて説明していきます。
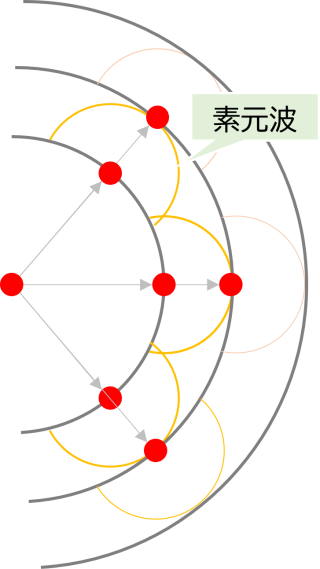
ホイヘンスの原理の基本は、"波"を細かく見ていくと、ある地点においてはそこから新たな"波"が全方向に発生※2しているということです。言葉でいっても分かりづらいので絵で説明します。(しかも、ちゃんとした絵を作るのが結構難しいのでかっこ悪い図なのはご容赦を・・・)
人間から見えるのは大きな波(図のグレーの線)です。しかし、大きな波の一点(赤色の点)を取り上げると、実はその点から新たに全方位に波が発生している、これがホイヘンスの原理の基本です。この波から切り取った小さな一点から発生する波を素元波と呼びます。そして、さらに素元波の一点を取り取り上げれば、そこからまた素元波が発生しているのです。見た目は大きな波であっても、細かく見ると波は小さな素元波の集合体である、というのがホイヘンスの原理です。人間から見える大きな波は、様々なありとあらゆる素元波が重なり合って合成された結果なのです。素元波が重なって強め合う箇所では波が高くなり、弱め合う箇所では波が低くなる、その結果が大きな波として見えているわけです。
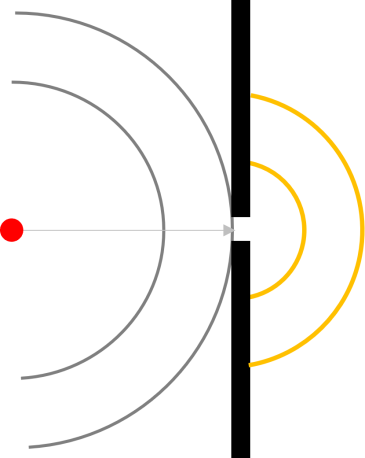
素元波が目に見えるのが回折という現象です。ある波が小さなスリットを通過するとき、スリットをすり抜けた波はすり抜けた平行な波が真っ直ぐ進んでいくのではなく、その点から波が左右にも広がります。おそらく物理の時間やなんかで、似たような図を見たことがありますよね。波を小さく切り取っても、そこから波が広がっていく。これこそが素元波の存在を証明しています。回折は至る所で見られます。海水浴の季節は終わってしまいましたが、例えば海水浴エリアである消波ブロックの裏側でも(弱くなっているけど)波があるのは回折によって波が回り込んでいるからです。
波は真っ直ぐだけを通るわけではない
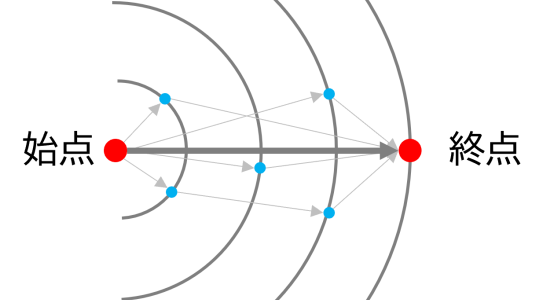
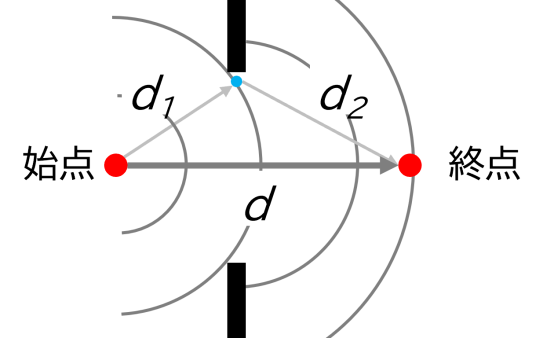
さて、ホイヘンスの原理から波の伝わり方を考えた場合、真っ直ぐに進んでいるように見える波でも、中身は真っ直ぐに進んでいる波だけではない、ということが見えてきます。素元波(下の図の青点)から波はいろいろな方向に広がり、次の場所でまた新たな素元波が発生する訳ですから、図のようにいろいろな経路を通って波は終点まで到達する、ということがく分かります。そうであれば、終点での波高は含む様々な経路を取った波、すなわち素元波が合成された結果と言えるでしょう。
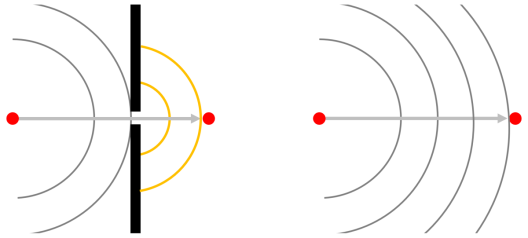
ところで、また回折の話に戻ります。下の図をご覧下さい。左右どちらも正面方向は開いていて波は届きますが、終点にはどちらの波が「強く」届くと思いますか?普通に考えれば、これまでの話がなかったとしても感覚的に右と答えるでしょう。そして、それはもちろん正解です。左はスリットによって波の大部分が遮蔽され、一部しか届きません。そして、スリットから回折で広がってしまうわけですから波のエネルギーは拡散してしまっているのです。ホイヘンスの原理の観点で見ると、左はいろいろなルートを辿ってきて届くはずだった波の多くが届いていないから右に比べ波が弱くなっている、とも言えるでしょう。
さて個々で一つの疑問が生まれます。スリットを広げたらどうなるのか?そこまでどこまでスリットを広げれば右と同じ強さになるのか?波が様々なルートを辿るのであれば、影響が無視できるまでにするには、スリットを相当に広げないといけない・・・ どのように考えればいいのでしょうか?この質問の答え(の一つ)がフレネルゾーンという考え方です。
フレネルゾーンとは?
フレネルゾーン
ホイヘンスの原理によれば2点間を伝わる波は考え得る全てのルートを通って来た波の合成になるわけで、理論上のルートは無限に考えられるはずです。だから、先の質問「スリットをどこまで広げたら右と同じか」の答えは、厳密に言えば「どこまで広げても絶対に同じにはならない」ということになります。しかし、ここは数学じゃなくて物理の世界です。波を考えるためには実用上「これぐらいであれば同じと考えて良い」という答えが必要です。距離が長くなればなるほど波は減衰するわけですから、その減衰を考えれば終点での強さに影響を与えられる範囲というのはあるはずです。
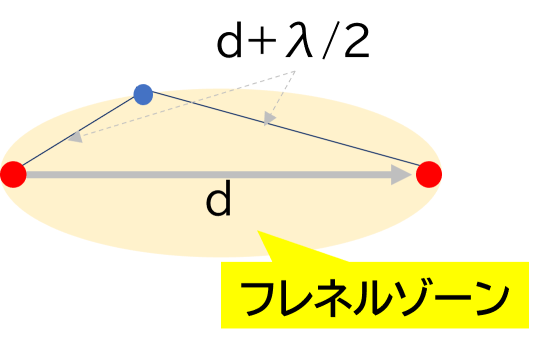
と、もったいぶって書きましたが、その答えは意外とシンプルです。完全に直進した波と、始点と終点の距離と比較し半波長分長い距離を伝わって終点まで伝わってきた波が合成した場合、波の形が完全に逆になりますので波は打ち消し合う形になります。下の図5でいえば、d1 + d2 = d + λ/2(λ:波長)となるポイントです。ここは一種のヌル点ですので、影響範囲という面ではわかりやすい最初の区切りとなります。
そして、実際のところもスリットをこの範囲まで広げれば、終点の波の強さにあまり影響を与えなくなる(=スリットがないのと変わらない)ことが分かっています。そのため、電波や光を扱う上ではここよりも外側のことは考えなくて良いとされています。これは「正規分布で何%がここに入る」といった数学的なアプローチで決まった範囲というよりも、ヌル点というわかりやすい区切りと実測や経験によって決められた範囲です。
この範囲は、言い換えると波の経路が「始点、終点間の距離+半波長以下となる範囲」の中に障害物があった場合には終点での波の強さに影響が出て、その範囲外であれば影響は無視できることを意味します。そしてこの「影響が出る範囲」のことはフレネルゾーン※3と名前が付けられています。フレネルゾーンの定義「始点、終点間の距離+半波長以下になる範囲」というのは、始点と終点から距離の和が一定(始点終点間+半波長)となる図形の事を意味します。これは、すなわち「楕円」の定義となりますので、フレネルゾーンは必ず楕円となります。
平面で見ると楕円ですが、当然のことながら音や光、電波では三次元に伝搬しますので、フレネルゾーンは立体の楕円、すなわち楕円体(回転楕円体)となります。
このフレネルゾーンの中に障害物があると、基本的に波は減衰します。減衰量については、波長はもちろん、障害物はどこにどれだけあるかということが重要なため定量的なものが出しにくいのですが、フレネルゾーンの半分の体積が潰れると、1/4(6dB減衰)になるということは分かっています。また、電波ですと反射などでフェージングが発生するわけですが、これが発生するかしないかを、地面とか壁など、反射面がフレネルゾーン内に入っているか入っていないかで判断することもできます。
フレネル半径
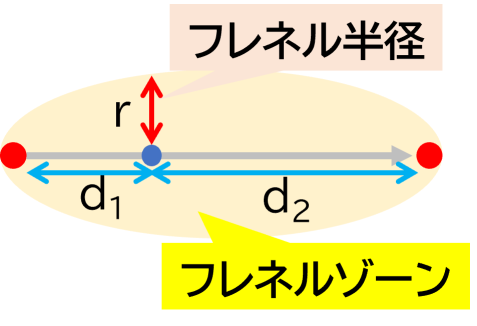
さて、電波通信とかで実際の現場でフレネルゾーンを考慮する場合、「楕円ですよ」と言われてもどこが楕円の範囲内で、どこが範囲外なのかを現場で判断するのは難しいものです。しかし、楕円だからこそ始点、終点からの距離が分かってしまえば、その点の半径というのは計算で求めることができます。それをフレネル半径と呼んでいます。例えばアンテナの高さ10mで求めたい場所のフレネル半径が8mだった場合、その場所ある障害物の高さが2m以上だった場合にフレネルゾーンに引っかかる、ということが分かります。
このフレネル半径は、比較的簡単な計算で出すことができます。詳しい計算の過程は近似とかが入るため説明が大変なので省きますが、フレネル半径(r)を求める式はこの様になっています。
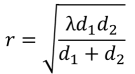
図7:フレネル半径の式
楕円ですから、2点間の中間点のとき、すなわち d1=d2 の時にフレネル半径は最大となります。単に「フレネル半径」と言ったときはこの最大値を指すこともあります。この最大のフレネル半径を算出する式は、上の式が更に簡単になってこうなります。
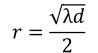
図7:フレネル半径の式(最大)
フレネル半径と光無線通信
さて、この式から例えば距離100mの場合の最大のフレネル半径を見てみましょう。(周波数もフレネル半径おおよその値です)
| システム | 周波数[MHz] | 最大フレネル半径[cm] |
|---|---|---|
| FMラジオ | 80 | 970 |
| 地上波TV | 500 | 390 |
| 携帯電話(プラチナ) | 900 | 290 |
| 携帯電話(メイン) | 2,100 | 190 |
| Wi-Fi(bg) | 2,400 | 180 |
| 5G(Sub6) | 3,600 | 140 |
| Wi-Fi(ac,6) | 5,300 | 120 |
| 5G(ミリ波) | 27,000 | 50 |
ざっとこんな感じです。結構大きいとみるか小さいとみるか個人差はあると思いますが、確実に言えるのは、例え周波数の高いミリ波であっても、ちょっとした「隙間を通す」というのは難しいというのが分かると思います。
さて、光のフレネル半径はどうなるでしょう。例えば弊社のLEDバックホールが使っているのが波長850nmの近赤外線。これでも光としては波長が長い方にあたりますが、これを周波数に直すとおよそ350THz。よく分からないですね・・・ とりあえず、上の式の当てはめて計算するとこうなります。
| システム | 周波数[MHz] | 最大フレネル半径[cm] |
|---|---|---|
| LEDバックホール | 350*10^6 | 0.46 |
つまり4.6mm。LEDバックホールのレンズの直径が10cmなのでレンズの方が大きい。これならフレネル半径はほぼ無視して良いという訳です。どんな狭い場所、天井裏でも、建物の隙間でも、ちょっと開いた扉からでも、相手側からレンズが見えていれば通信できる、これが光無線通信の特長の一つです。
おわりに
フレネルゾーンの理論から、なぜ光無線通信が狭い隙間さえあれば通信できるのかを説明いたしました。ホイヘンスの原理は高校の物理で習った記憶がある方が多いと思いますし、あの回折の図だけを記憶していた方も多いと思います。ですが、実はあれは「波が直線に進むだけではない」ということを表す原理でもあったのです。
今回は細かいことを沢山書きましたが、まずは「光無線通信でフレネルゾーンを考慮する必要は無い」とだけ覚えて頂ければ幸いです。
※1; レンズを薄くするため同心円状に分割し構成したレンズ。詳しくはこちらから。
※2; 「全方向に発生」の意味は、全方向に均等に波が発生(拡散)しているわけではなく、波の進行方向からの角度によって減衰する波であると定義されている。進行方向の逆側、つまり後ろ側の波の強さは0となる。
※3; 正確には第1フレネルゾーンである。フレネルゾーンは半波長毎に第2、第3と存在する。しかし、伝搬に大きく影響するのは第1のみであり、厳密な計算が必要である等特段の理由が無い限り使われないため、多くの場合単にフレネルゾーンと呼ぶと第1フレネルゾーンの事を指す。