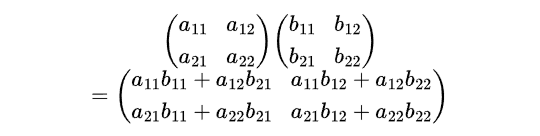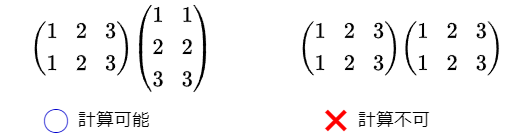LED通信事業プロジェクト エンジニアブログ
F#で行列計算をしよう #5
内積を計算する
記事更新日 2025年4月15日
はじめに
Microsoft F#は、Microsoft .NETグループの一言語であり、.NETで唯一の関数型言語です。関数型言語は副作用が少なく、その結果、完成したコードのエラーが少ないというメリットがありますが、それ以外にもう一つメリットがあります。それは、関数型言語は「行列計算を駆使したDeep Learning系AI処理を書きやすい」ということです。
しかし、F#で行列計算をしようと思っても、Microsoftの公式リファレンス程度しか見当たらず、しかも、それすらまともな解説も使用例もないため、折角の高機能が活かされていません。調べても誰も書いている様子がありません。仕方なく私が作るしかないと考え、F#で行列の計算をする方法を何回かに分けた連載という形でお伝えしようと思います。
真面目に最初から読むというよりは、F#を調べているときに検索に引っかかれば良い、という程度の記事にしていくつもりです。なぜなら、このようなニッチな内容は、AIでは「正しいか正しくないか」の判断が難しいことが多いため、このような記事もあれば、誰かの役に立つのではないかと考えています。
ちなみに、AIそのものの作成方法(誤差逆伝播法など)や、行列計算そのものの意味(意味や計算方法など)、そういったものの説明はしません。そもそも、そのような大層な内容ではなく、あくまで「プログラミング中に困って検索したら引っかかる」ことを目的としています。
今回は、F#で内積の計算をしてみます。内積は、ベクトルや行列の計算で出てきますが、行列で構成されるAIの計算で多用されています。F#で「内積」はどうやって計算するのか?どうやるのが良い方なのか?色々と調べていきます。
内積とは?
さて、改めて内積についてですが、行列計算で最も使う計算の一つが「内積」だと言えると思います。AIの計算でも度々出てきます。これから、その内積をF#で計算するならどういった方法が良いのか、というのを調べていきたいと思いますが、もしかしたら、内積という計算を知らないという人もいるかも知れません。すぐ上の"はじめに"で「計算そのものの意味は説明しない」と書きましたが、今回は内積という計算自体を取り上げるので、最初に説明を入れされていただきます。
内積の計算
内積の計算は、下図の通りです。前の行と後ろ列をかけるというちょっと特殊な計算ですね。どうしてこのような式なのか?と言われると説明は難しいのですが、内積とはこういう計算式なんだと思って受け入れて下さい(おそらく学校で習うときも強制的に覚えさせられます)。
図の例は2x2行列の内積です。内積では前の行列(かけられる行列)の列数と、後ろの行列(かける行列)の行数が合っている必要があります。そうでないと内積は計算できない、という数学上のルールになっています。例えば、前の行列が2行3列だとしたら、後ろの行列は3行2列のような3行をもつ行列でないと内積を求めることが出来ません。これは、正方行列(行数と列数が同じ行列)でないかぎり、同じ行列同士の内積は計算できないということを意味します。これが、内積の特殊なところでもあります。
私のようなおっさんの時代だと、文系高校生でも行列、ベクトルの学習は必須だったので、今更内積の計算の説明をする必要なんて無かったんですよね。でも、最近の文系大学生や若い社会人だと、行列やベクトルを全く習っていないという人もいるみたいなので、最低限の説明だけ付けておきました。ちなみに、現在現役の高校生だと、行列、ベクトルが復活しているようですが、かつてのようにガッツリやるわけではないみたいです(もし違ったらすいません)。
内積の使い方
とは言え、例え高校で行列が必須だった人も、内積計算の意味や用途を教わることはほとんどないので、内積を使うのは直交しているかどうかを判断するときだけ、という人が大半でしょう。かく言う私も、そうでした。しかし、コンピューターの世界では内積が使われることが意外と多いです。例えば、ポリゴンゲームの「当たり判定」には、2点の内積が使われる事が多いです。内積は2点の位置(角度)関係をあらわすことが出来るからなんですよね。そして、AI関連の計算においても、内積は必須になっていると言っても良い状況なんです。
例えば、Deep Learning等で使われるニューラルネットワーク(NN)においては、回答へ近づけていくための勾配への重み付けに内積が使われます。それどころか、NNの各段(パーセプトロン)にて内積が行われるのが基本なので、NNにおいては内積が最も使われる計算の一つと言って良いでしょう。また、LLM(生成AI)においてはTransformerのQKV注意機構(アテンション)で内積が多用されます※1。Transformerにおいては単語(トークン)はベクトルで表されますが、その関連性を計算するのに内積が使われます。これは、前述の「ゲームの当たり判定」に似ている使い方と言えるかも知れません。
F#での内積計算
実際にF#で内積の計算する方法について考えます。この連載はF#が配列の計算に強く、AIに向いているということで始めたわけですが、一つ大きな問題があるんですよね。それは、F#の配列の標準関数には、内積の計算がないということです。内積自体はそこまで複雑な計算ではないので、自分で内積関数を作れば計算はできるんですけれども、どういったアルゴリズムが最適(最速)かはわかりません。なんで、内積という行列で最も使う関数が準備されていないのか、正直理解に苦しみます。しかし、ないものは仕方が無いので、今回も内積を計算するならどの方法が最適なのかを検証していきます!
検証方法
計算に使用する配列は、要素の中身ランダムの正方行列(行と列が同じ数の行列)とします。AIに使う行列は正方行列じゃないことの方が多いですが、列数、行数を判断するとかは本題ではないため、今回はご容赦下さい。検証としては、この正方行列のサイズと計算回数を変えて、計算時間を測る、ということをします。
今回用意した内積の計算方法(アルゴリズム)は、以下の3つです。
- 力業(個々の要素に直接アクセス)
- スライス+MAP2関数を使用
- NumPyDotNetを使用
それぞれにおいて、計算速度を測ります。結果は最後に紹介しますので、まずはそれぞれの計算方法の特徴とコードを紹介しようかと思います。
1. 力業(個々の要素に直接アクセス)
さて、最初の計算方式は、1つ1つの配列要素にアクセスして、内積を計算するという方法です。For文と多用し、単純に要素毎に計算を繰り返すという力業です。数学の公式通りに実装した、はっきり言えば「工夫のない」方法です。
これまでの経験から、個々の要素にアクセスするため、おそらく計算は遅くなるであろうと想定しています。しかし、主要生成AI(ChatGPT、Gemini、Copilot)に聞くと、多少ループ方法の違いはあれど、すべてこの方法を推奨してきます。つまりは、最も基本的で確実な方法だとも言えるんでしょうね。
/// 内積サンプル1
/// 個々の要素毎に計算
let dotTest1 (ary1:double[,]) (ary2:double[,]) =
let maxx = Array2D.length1 ary1 //配列の1辺の長さを求める(正方行列のみ)
let ansAry = Array2D.create maxx maxx 0.0 //結果入力用の配列
// 要素毎にfor文で計算
for y in [0 .. maxx - 1] do
for x in [0 .. maxx - 1] do
let mutable elem = 0.0
// 行方向x横方向を1要素毎に計算
for i in [0 .. maxx - 1] do
elem <- elem + ary1[y, i] * ary2[i, x] //要素毎の計算
ansAry[y, x] <- elem
ansAry //戻り値
2. スライス+MAP2関数を使用
今度は、スライスとMAP2関数を使用します。以前の要素同士の計算の回にて「Map2関数が要素毎足し算より高速」であり、2次元配列を1次元に変更する回で「要素数が多くなるほどスライスの効果が高い」ということがわかっています。これを両方使って内積を計算します。
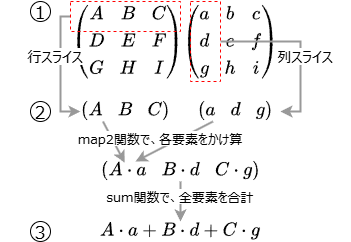
具体的な計算は
- 行と列をスライスして、それぞれ1次元配列を抽出する
Array.map2関数を使って、各要素を掛け合わせた1次元配列を作成Array.sum関数を使って、全要素を足し合わせる
言葉で書くより、下の図を見て貰った方が早いかも知れません。
この計算のポイントは、個々の配列要素を指定しての計算を一切使わないところです。かけ算も足し算もF#の1次元配列関数を使用することで、高速化を図っています。この方法、スライスとMAP2が高速であることを過去に実証している著者ならではの自信作です。どの生成AIも、この方法を思いついてはいないようですが、おそらく力業よりは速くなるはずです。
/// 内積サンプル2
/// スライスをしてMAP2する
let dotTest2 (ary1:double[,]) (ary2:double[,]) =
let maxx = Array2D.length1 ary1 //配列の長さを求める(正方行列のみ)
let ansAry = Array2D.create maxx maxx 0.0 //結果入力用の配列
// かけ算を行う関数(map2関数で使用)
let multi x y = x * y
for y in [0 .. maxx - 1] do
let rowAry = ary1[y, *] //ary1の1行をスライス
for x in [0 .. maxx - 1] do
let newAry = Array.map2 multi rowAry (ary2[*,x]) //map2で要素毎にかけ算
let elem = Array.sum newAry //全要素を足し算
ansAry[y, x] <- elem
ansAry //戻り値
3. NumPyDotNetを使用
3つめは、ちょっと反則技かもしれません。
皆さんもご存じとは思いますが、現実のAI実装ではPythonが使われることがほとんどです。そして、AIにPythonが使われる理由の一つがNumPyだと言われています。Python単体では行列計算が強いわけでも、高速なわけでもないんですが、PythonにはNumPyというライブラリが存在していて、これを使うと強力かつ柔軟に、それでいて高速に行列計算が出来るようになっています。NumPyの存在こそがPythonの強みな訳ですが、それ故にAI関連のコードをPythonで書いている全員(本当に100%全員)がNumPyを使っていると言えます。ですから、PythonというかNumPyがAIコーディングのデファクトスタンダードになっていて、行列の計算方法とかもNumPyありきで考えられています※2。
AIの世界ではアウトサイダーなMicrosoft .NETでも、当然NumPyと同じような方法で行列を扱いたいという需要は多いわけで、そうすると、NumPyを.NETでも使えるようにする人が出てきます。今回使うのは、そういったものの一つである"NumPyDotNet"というライブラリです。NumPyDotNetを導入すると、NumPyを.NETで扱えるようになり、NumPyの機能のほとんどが使えるようになります。
ちなみに.NETには"NuGet"という恐ろしく簡単なライブラリ(パッケージ)の導入ツールがあるため、外部ライブラリを簡単に導入できます。Visual Studioで[プロジェクト]-[NuGetパッケージの管理]を選び、そこからNumPyDotNetをインストールするだけです。NumPy関連のライブラリはいくつかありますので、別にどれを使っても良いとは思いますが、今回は私が以前から使っているNumPyDotNetを使用させていただきます。
さて、前置きが長くなりましたが、私がなぜわざわざNumPyのライブラリを導入するのかと言えば、それはNumPyには内積を計算する関数があるからです。内積を計算するのにFor文もスライスとかの小細工も必要ありません。dotという関数一発で計算できます。尚、NumPyDotNetは、NumPyのソースコードを.NET用に100%移植したもの(by 作成者)だそうです。ですから、高速と言われているNumPyを使うので、きっとF#でも内積を高速に計算できるはず。
ただ、一つ問題があり、NumPyで内積を計算するとndarrayというNumPy内部の変数型になってしまいます。NumPyの内部では配列は常に1次元配列であるため、NumPyのndarray型を、F#で扱えるarray型に変換すると、1次元配列になってしまうのです。すべてNumPyで完結するように作っていればそれで問題ありませんが、今回の趣旨は、あくまでF#上での計算です。そのため、計算コードでは1次元配列を2次元配列へ変換するようなコードが追加されています。そして、この部分が時間のロスとなる可能性があります。まあ、それも含めて、検証してみます。
/// 内積サンプル3
/// NumPyDotNet
let dotTest3 (ary1:double[,]) (ary2:double[,]) =
let maxx = Array2D.length1 ary1 //配列の長さを求める(正方行列のみ)
let ansAry = Array2D.create maxx maxx 0.0 //結果入力用の配列
// NumpyDotNetのnp.dotを使用し内積を計算
let ansnpAry = np.dot(ary1, ary2)
let ansAry1D = ansnpAry.AsDoubleArray() //F#用配列に変換(1次元配列)
// 1次元配列を2次元配列へ戻す(スライス活用版)
for i in [0 .. maxx - 1] do
let lowx = maxx * i
let highx = maxx * (i + 1) - 1
ansAry[i, *] <- ansAry1D[lowx .. highx] //スライスして行毎に代入
ansAry //戻り値
検証結果
以下が検証結果です。結果の単位はすべて"秒"です。
| 行列サイズ 計算回数 |
16x16 100,000 |
64x64 10,000 |
256x256 500 |
1024x1024 3 |
2048x2048 1 |
|---|---|---|---|---|---|
| 力業(要素毎) | 4.7 | 26.7 | 88.0 | 78.4 | 226.5 |
| スライス+MAP2 | 2.5 | 13.8 | 46.6 | 56.5 | 166.0 |
| NumPyDotNet | 13.1 | 13.3 | 10.9 | 14.1 | 44.0 |
要素毎に計算するよりは、スライス+MAP2の方が常に計算は速いようです。しかし、16x16という小さい配列での計算をのぞき、F#そのままよりも、NumPyDotNetを使った方がが圧倒的に速いことがわかりました。AIの計算で16x16なんて計算使いません。それどころか、Aiでは馬鹿でかい行列の計算が基本になりますので、実質はどんな状況に置いてもNumPyDotNetの方が早いという結果といえるでしょう。いや、これじゃあF#意味ないじゃんか・・・
NumPyDotNetとF#の計算で、どうしてここまで差が出たのかをちょっと考えてみましたが、どうもこれはCPU使用率の差のようです。要素毎にせよ、スライスにせよ、F#そのままの計算だとCPU使用率が20%程度までしか上がらないのに対して、NumPyDotNetの場合は65%程度まで上がっていました※3。そう考えると、同じCPUの利用率ならば、スライス+MAP2とNumPyDotNetの差はそこまで大きくはないのではないか?という疑問が湧いてきます。そう考えると、この差を埋めるために、F#をマルチスレッドにして、CPU利用率が高くなるようなコーディングにする必要がありそうです。
まとめ
いかがだったでしょうか?純粋なF#の計算よりも、外部のNumPyDotNetを使った方が速いというのは、私的にはなんとも残念な結果でした。更なる高速化のためには、Microsoftが配列の内積の計算関数を実装してくれるのが一番※4ではあるものの、残念ながらこの現状で実装されるとは期待できません。
このままでは悔しいので、次回は「F#でCUP利用率を無理矢理上げて計算すれば、NumPyDotNetを超えるのか?」というテーマでやっていきたいと思います。それでは、次回をお楽しみに。
※1; 当然、Transformer内のFFNN(Feed Forward Neural Network)においても、DLと同じように内積が多用される。
※2; NumPyをベースに、GPU(CUDA)を使えるようにしたCuPyも使われる。そのCuPyを.NETで使用できるようにしたCuPy.NETというパッケージも存在するが、今回は使用しない。
※3; AMD Ryzen7 Pro 4750U(1.7GHz 8コア16スレッド)使用
※4; ゲームプログラミング用のプラットフォームである"Unity"には、内積計算が存在する。