LED通信事業プロジェクト　エンジニアブログ

CRCってなに？

高校生でもわかる通信用語 #2

記事更新日 2023年10月10日

---

はじめに

社内の人間に、「今までのブログは難しすぎて専門家しか読まないよ」と指摘され始めた「高校生でもわかる通信用語」シリーズの第2回です。できるだけ難しい言葉を使わずに、できるだけわかりやすく通信用語を説明していきたいと思います。

今回は、CRCについてです。名前はあまり知られていませんが、携帯電話にも、Wi-Fiにも、イーサネットにも、現在使われているほとんどの通信で使われています。CRCってなに？どんな役割なの？どんな仕組みなの？そんな事を説明していきたいと思います。前回の「レイヤー2」は説明内容も多くちょっと長すぎたため、今回はもう少し短めです。

エラーを発見する

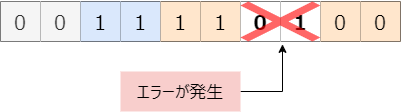
デジタル通信で一番大事な事って何でしょう？　速いこと？エラーが無いこと？　いえいえ、どちらでもありません。一番大事なのは「送られたデータが正しいか、正しくないか、わかること」です。

実は、どのような通信であろうともエラーを完全に0にすることはできません。実用上ほぼ無視できるほどエラーを少なくすることはできますが、完全に0にはできません。その理由は、雑音（ノイズ）が0にはできないから。雑音がある限り、確率的に必ずエラーが発生するんです。これは物理法則であり、覆すことができません。だから、ありとあらゆる全ての通信システムはエラーが発生することを前提に設計されなければいけません。これは、我々の目に見えているLANケーブルだったり、Wi-Fiだったりだけじゃなく、コンピューターやスマホの”メモリとCPU間”など極小型の装置内部の通信でも同じ事です。

というのも、デジタルデータっていうのは1ビットでもエラーがあると、それがバグとなり致命的な問題になります。プログラミングやっている人ならわかりますが、プログラミングコードって1文字間違っていただけで正常に動きませんからね。多くの言語では大文字と小文字の違いすら許されないんですよ。だから、通信で1ビット0と1が入れ替わってしまったってだけで、多くのプログラミングコードは動かなくなります。音声とか動画とか、言わば垂れ流しデータだとエラーが許容される場合もありますけど、アプリなんかだと、例えば10GBぐらいある超大作巨大ゲームでも、1ビットエラーがあるだけで動かなくなる可能性があります。

だから、通信で絶対に必要となるのが「エラーと思われるデータを排除する」こと。そのためには、エラーがあったかどうかを発見できることが重要なんです。エラーさえ発見できれば、エラーが発生したということがわかれば、後はどうにでもなります。例えば、エラーだったパケットをもう一回送って貰うとか、そんな事で済みます。というわけで、ここまで長々話してきたエラーの話は、「エラーが問題なんじゃない、エラーかどうかわからないことが問題」って、どっかで聞いたような台詞でまとめられるのでした。

エラーを発見する方法

繰り返し

エラーを発見する方法は、誰でも簡単に思いつくんです。例えば、同じデータを必ず2回送ること。

2回送ったデータが一致していればエラーが無い、どこか一致していなかったらエラーがありって判断。確かに、確実にエラーが発見できそうだ。仕組みも単純。実はこの方法、古来よりいろいろなところで使われています。皆さんも使ったことがあるばず。どこで使われているかって？　聞いたことありますよね、「復唱」って言葉。「大事なことなので二度言いました」って。この方法、生身の人間の会話のみならず、デジタル通信においても効果もあるんです。仕組みも簡単ですし、効果も大きい。だけど、一つ大きな問題があります。同じデータを2度送るって、とても無駄なんですよね。大事な通信速度の半分をドブに捨てなければならず非効率。特に、エラーがそれほど発生しないであろう有線接続とかの環境では、はっきり言って全くの無駄。なので、繰り返しっていう方法は、エラーのとても多い無線通信で希に使われることもあるんですが、通信全般で広く使われている方式ではありません。とはいえ、人間は積極的に使ってください。復唱、伝達ミスを無くすのにとても大事ですよ。

パリティチェック

次に、もう少し無駄の少ない方法を紹介します。例えば、データが8ビットあるとします。この8ビットのデータのうち「1の数が奇数だったら1というビットを追加」、「1の数が偶数だったら0というビットを追加」、とします。

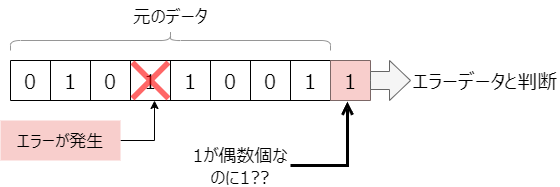
もし、受信した時に何のエラーも無かった場合、前8ビットの1の個数と最後の計算結果のビットが一致するはずです。だから、このデータは正常である、つまりエラービットはなかったと判断されます。

一方で、ある1ビットがエラーになると、最後のビットとの計算結果が合わなくなるため、エラーである事がわかります。どこのビットにエラーが発生したかまではわかりませんが、この9ビットの中のどこかにエラーがあったことは確実ですので、この9ビット全てがエラーとされ破棄されます。

この方式は、8ビットが9ビットになるだけでエラーが発見でき、とても効率が良いです。また、エラー発見のための計算も極めて単純なため、実装も簡単です。この方式はバリティチェックと呼ばれていて、追加した最後のビットをパリティビットと呼んでいます。ちなみに、今回はデータ中の1の個数が奇数の場合にパリティビットを1としていましたが、偶数の場合を1としても同じ事です^※2。

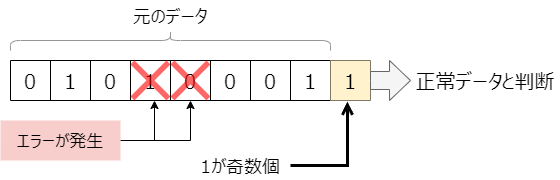
単純で、無駄も少ないこのパリティチェックというシステムですが、大きな問題があります。勘の良い方はお気づきかも知れませんが、このシステムは2ビットエラーが出るとエラーを見落とすという性質を持っています。

2ビット、というか偶数ビットのエラーが出てしまうと、エラーが発見できなくなる。これが意味するところは「パリティチェックはエラーの多いところでは使えない」ってこと。元のデータの長さは、7か8ビットのことが多いため、それプラスパリティビットで計、8～9ビットの中で2度エラーが出てはいけない、って事になります。これって、一見簡単そうですが実は結構厳しい条件で、エラーが発生する確率（エラー率）が相当低い通信じゃないと実現できません。そのため、コンピューター内部の通信の様なエラー要素が極めて少ない区間では広く使われているものの、エラー発生確率が高い距離の長い通信や、エラー頻発の無線通信では使うこととができません。昔は、RS-232C^※1の様なPCと周辺機器間の通信でもパリティチェックが使われていたのですが、現在のPC周辺機器はほぼ全てUSBに置き換わってしまいましたので、パリティチェックを使っている外部機器というのは少なくなりました。Tera Termよく使ったな～（遠い目）。

チェック・サム

パリティチェックをちょっと高級にしたチェック・サムという方法があります。原理はパリティチェックとほぼ同じで、データを全て足してその合計値をチェックに使うというものです。

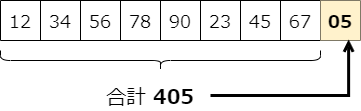
チェック・サムの仕組みは簡単で、まず元データの全ての値を単純に合計します^※3。図の例では、データ部分を全て足すと合計は405となります。で、データに合計値405の下二桁の05だけを付ける。これで、もしどこかの値が変化してしまっていても合計値と合わなくなるため、エラーが検出できるというわけです。やっていることはパリティチェックの拡大版なので、処理も簡単で、エラーを発見する能力が高いためパソコン等でよく使われます。チェック・サムはプログラミングでも作りやすい（コードを書きやすい）ので、例えばダウンロードしたファイルのエラーチェックにも使われます。

しかし、弱点もあります。それは、順番の入れ替わりが検出できないこと。a + b = b + aですよね？数ビットの小さいデータなら入れ替わる可能性って低いですけど、ある程度サイズのあるデータがインターネットのような通信経路が複数取れる経路を通った場合には、順番が入れ替わってしまう可能性があります。また、複数のエラーによってどこかの値が+1になって、どこかの値が-1になるってパターンも可能性は低いですが考えられます。結局も、これも順番が考慮されていないことの弊害の一つです。

このように、これまで見てきたエラーの発見方法は、簡単ではあるものの何かしらの弱点があり、特にエラー発生の確率が高い通信では十分な能力ではないことがわかります。もちろん、それぞれ使い道はあり、今も使われている方法ではあるのですが、もっと何か決定的な方法はないのでしょうか？

と、もったいぶった書き方しましたが、まあ当然あるんですよね。今までの弱点を全て克服しているエラー発見方式が。それが、今日のテーマであり、これから紹介するCRCです。

エラー発見の決定版、CRC

CRCは、略さずに言うとCyclic Redundancy Check、日本語で言うと「巡回冗長検査」です。言葉だけ聞くとなんのこっちゃ？って感じですが、名前はともかく、CRCは現在のところエラーを発見するのに最高のシステムと言われています。（これまで紹介したものよりは複雑ですが）比較的簡単な計算で、尚且つエラーを発見する性能が高く、エラーが複数あっても、連続していても、順番が入れ替わっていても発見可能。素晴らしい。CRCは、現在ありとあらゆる通信に使われていますが、それは何と今から60年以上前にW.ピーターソンというアメリカ人が発明したものなのです。コンピューターどころか電卓も無い時代に発明したものが、今尚主力として使われ続けているって、ちょっと想像できませんね。

さて、CRCの仕組みは比較的簡単なんですが、論理演算というやつを勉強していないと理解ができません。ANDとかORとかの論理演算、我々おっさんは大学で勉強しましたが、今は高校の情報という授業でやるんですよね。今後、共通テストでも採用されるとか。時代は変わった。論理演算を習った人のために簡単に説明します。まず、後ろにCRCビットなるビットをくっつけます。そして、ある数値（下の図では101）があって、これを使って元データが0になるように、上の桁からXORしていきます。繰り返していくと、データはどんどん0になっていきデータを全て0にしたとき、追加したCRCビットに0にできなかった数値が残ります（下の図では01）。これが計算結果としてのCRCビットであり、このCRCビットを計算前の元データにくっつけて完成です。文字で書くとわかりにくいですが、図を見て貰えば複雑なことをしていないことがわかっていただけると思います。

この計算、一体何をやっているのかというと「割り算」です。そして追加したCRCの部分は割り算の「余り」を意味します。CRCは、実は割り算の余りを計算しているのと同じになるのです。割り算なので、値が変わっても、連続エラーがでても、そして順番が入れ替わっても、答えは変わってしまいます。まあ、理論的には色々あるんですが、とにかく、CRCは「割り算をするからエラー発見能力が高い」とだけ覚えておいてください。尚、実際に使われているCRCビットは16ビットや24、32ビットなど結構長いものなので、10000（10キロ）ビットを超えるような長いパケットであっても、エラーを検出することができます。

CRCは、これまで説明したどのシステムよりもエラーを発見する能力が高いですが、それと同時にこれまで説明したどのシステムよりも計算負荷が高いです。まあ、当然ですね。説明の図もこんなに縦長なわけですし、計算量の多さはわかっていただていると思います。それでも、その計算量に見合った発見能力なので、CRCは様々なシステムに採用されています。いま、画面にこのブログが表示されているのもCRCのおかげであると言っても過言ではありません。

CRCがどこで使われているか?

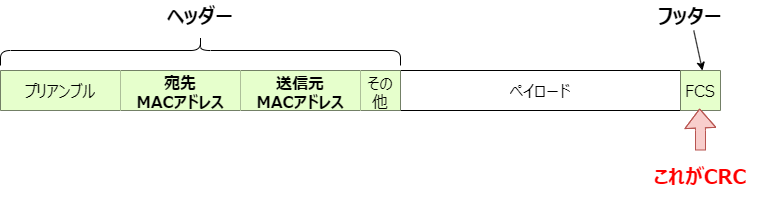
前回レイヤー2で出てきたイーサネットフレームを覚えているでしょうか？

イーサフレームはヘッダーとしてMACアドレスなどが付いていましたが、フッターにはFCSが付いていました。前回説明しませんでしたが、FCSはFrame Check Sequenceの略であり、これがまさにCRCの事を指します。つまり、イーサネットはCRCでエラーチェックをしているのです。それ以外にも、インターネット上のサービスでは、アプリケーションレベルのパケット（例えば画像を伝送するためのパケット等）に独自にCRCを付けて送受信する場合もあります。

イーサネットの拡張版であるWi-FiもCRCを使っていますし、携帯電話もCRCを使っています。5G（第5世代携帯電話）では2重にCRCを掛けることもあります^※4。また、USBもCRCを使っていますし、弊社光無線通信装置であるLEDバックホールもCRCを使っています。とにかく、現在思いつくようなデジタル通信はほとんどCRCを使っています。それぐらい、エラーを発見する能力が高く、効率的であるということです。

まとめ

ここまで、わかりやすさのため「エラーを発見」と書いてきましたが、通信用語的にエラーを発見することを誤り検出、英語でError Detectionと呼んでいます。誤り検出とかエラー検出って言うとちょっとお堅いので今回は避けてきましたが、ちゃんとした文章ではほぼ誤り検出、エラー検出と書かれているでしょうから、今後はこちらの単語を使っていただけくのが良いかと思います。

最後に一言。パリティチェックもチェック・サムも使われていますが、現在の通信、特にインターネット上の通信では「誤り検出=CRC」だと認識しても問題ありません。最初にも書きましたが、デジタル通信で最も大切なのはエラーを発見することです。だとすれば、インターネット通信で一番大事なのはCRCと言っても過言ではない！それほどCRCは重要な役割を担っているのです。

---